Echando la vista atrás, todos recordamos la manera en que aprendimos a multiplicar. Se podría decir que es de esas cosas que nunca se olvidan, ¿o sí? Siempre digo que la mejor manera de estar en forma con las matemáticas es practicando, pero es normal que con los años y la falta de ejercicio se vaya oxidando nuestra agilidad mental.
¿Por qué se nos olvida? De una manera u otra, casi todos aprendimos las tablas de multiplicar recitando sin parar, como una canción, hasta aprendérnoslas de memoria. Es de esos acontecimientos que marcaron nuestras vidas. Quien más o quien menos pasó algún momento de apuro cuando le preguntaban ese 7x8 y decía un tímido 64 para ver si acertaba.
Con este método, el de la repetición sin fin, no solo potenciamos el aprendizaje mecánico, también creamos obstáculos a la hora de fomentar el pensamiento lógico y el descubrimiento en los procesos de enseñanza. Por ello, es necesario poner en práctica algunos consejos que nos permitan salir de más de un apuro sin tener que utilizar la calculadora.
Nunca está de más buscar nuestros propios trucos a la hora de realizar las cuentas: dominar la suma encontrando atajos que me permitan alcanzar el resultado, transformar las cuentas desconocidas en una combinación de otras conocidas… Pero claro, todo esto es muy sencillo si estamos hablando de multiplicaciones simples. Para resolver multiplicaciones más complejas he encontrado un método práctico y visual que puede resultarnos muy útil. Se llama "multiplicación japonesa" y consiste en trazar líneas paralelas y perpendiculares en nuestro papel e ir contando sus puntos de intersección en un orden concreto. Una muestra de ello podéis encontrarla en el siguiente vídeo:
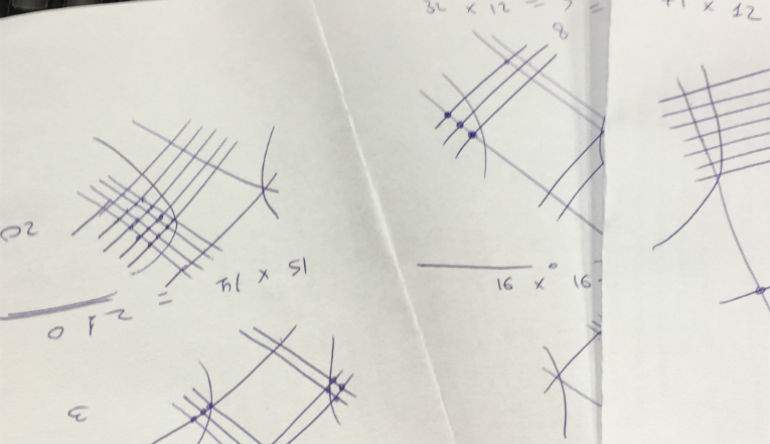
Como podemos observar, si queremos multiplicar 32 x12, lo que debemos hacer es ir trazando las líneas en función del orden de aparición en nuestra cuenta. En primer lugar, si nos fijamos en el 32, trazamos tres líneas paralelas agrupadas en una corta distancia y las dos siguientes también paralelas a estas, pero con un margen mayor respecto a las anteriores. Con el 12 hacemos lo mismo, pero esta vez empezando por el 1 y que esta línea corte perpendicularmente, formando un ángulo de 90 grados, a las dos agrupaciones previas por el margen izquierdo y con el 2, dos líneas paralelas a la anterior, pero perpendiculares a las otras por el margen derecho.
Escrito así suena un tanto complicado, pero en realidad es bastante sencillo; casi como un juego. Para terminar el proceso lo que tenemos que hacer es sumar los puntos que coinciden entre ellas e ir reflejándolos en el orden correspondiente.
Este método no es reciente, cuenta con siglos de antigüedad y funciona porque las líneas actúan como "marcadores de posición" y el número de puntos en cada intersección es un producto del número de líneas.
Puede resultar lento, no digo lo contrario, pero resulta muy divertido practicarlo.